Make a free body diagram from basic principles!
Watch The Video:
Other Demos of Interest:
 |
 |
 |
How a Pendulum Works |
How to use a Force Table |
How a Tippe Top Works |
Teachable Topics:
- Statics Friction
- Tension
- Vector Components
Theory:
Free body diagrams are a great way to simplify a complicated situation involving many different types and directions of forces. The forces can then be analyzed easily using Newton’s second law of motion. In this demonstration, a wood block is pulled up an inclined plane by masses hanging from a pulley attached to the ramp. See Figure 1 for a diagram of the demo set up.
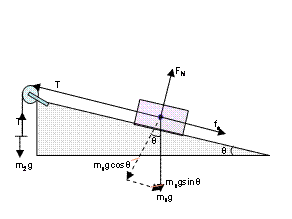
Figure 1: Detailed Free-Body Diagram
Free body diagrams show all of the forces acting on each individual mass in a system. The mass can usually be simplified to a dot representing the object’s center of mass, and the forces are then vectors extending out from the dot in the direction they are applied. A free body diagram for each mass is shown in Figure 2.
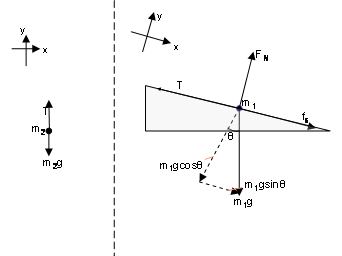
Figure 2: Left: mass hanger m2; Right: block m1
Many different types of forces are present in this demonstration. It is important to take note of the chosen directions of x and y in each of the free body diagrams – this is arbitrary and can be put in any direction that makes analysis easiest (note that in the case of m1 the x direction was chosen to be parallel to the face of the ramp so that the tension and normal forces are directly along each of the directions.)
To begin, each mass is acted upon by gravity, which acts straight down. This force is essentially the ‘weight’ of the object: Fg = mg where m is the mass of the object and g is the acceleration due to gravity (9.8 m/s2). However, since the object is inclined to the plane of the table, there will be components of the force of gravity in both the x and y directions.
Another force acting on m1 is the normal force which is the force exerted by the ramp onto the block to compensate for the force of gravity pulling the block downwards.
Tension, T, is the force exerted on the block by the string. It is directed along the direction of the rope and away from the object
The last force acting on the block is static friction, fs. Static friction is a force that tries to keep the object static, or motionless. This force must be overcome before the block will slide up the ramp. This is done by adding masses to the mass hanger. The magnitude of static friction depends on the material used and what is called, “the coefficient of static friction”. For example, a rough piece of wood would have a higher coefficient of static friction than a smooth piece of metal.
As shown in Figure 2, the only forces acting on m2 are the force due to gravity and the tension from the string.
Apparatus:
- Ramp (or piece of wood with one side elevated)
- Smaller block of wood to slide across ramp. The block must have a hook attached to one end so that a string can be attached.
- String
- Pulley
- Mass hanger
- Masses of various weights
Procedure:
- Set up the apparatus as shown in Figure 1. Make sure your mass hanger is light enough (or that incline of your ramp is large enough) so that the block doesn't slide across the ramp unless masses are added to the hanger.
- Add masses slowly to the mass hanger. Add small masses until you are able to overcome the static friction keeping the block from sliding and it slides up the ramp.



