How a Pendulum Works

A look at the physics that govern the pendulum.

Watch The Video:

Other Demos of Interest:

Wilberforce Pendulum	Newton's Cradle	Chaotic Pendulum

Teachable Topics:

• oscillatory motion
• conservation of energy
• free-body diagram

Theory:

A pendulum consists of a mass suspended from a string that is fixed to a pivot. The mass is free to swing back and forth, and rests at what we will call the “equilibrium position”.

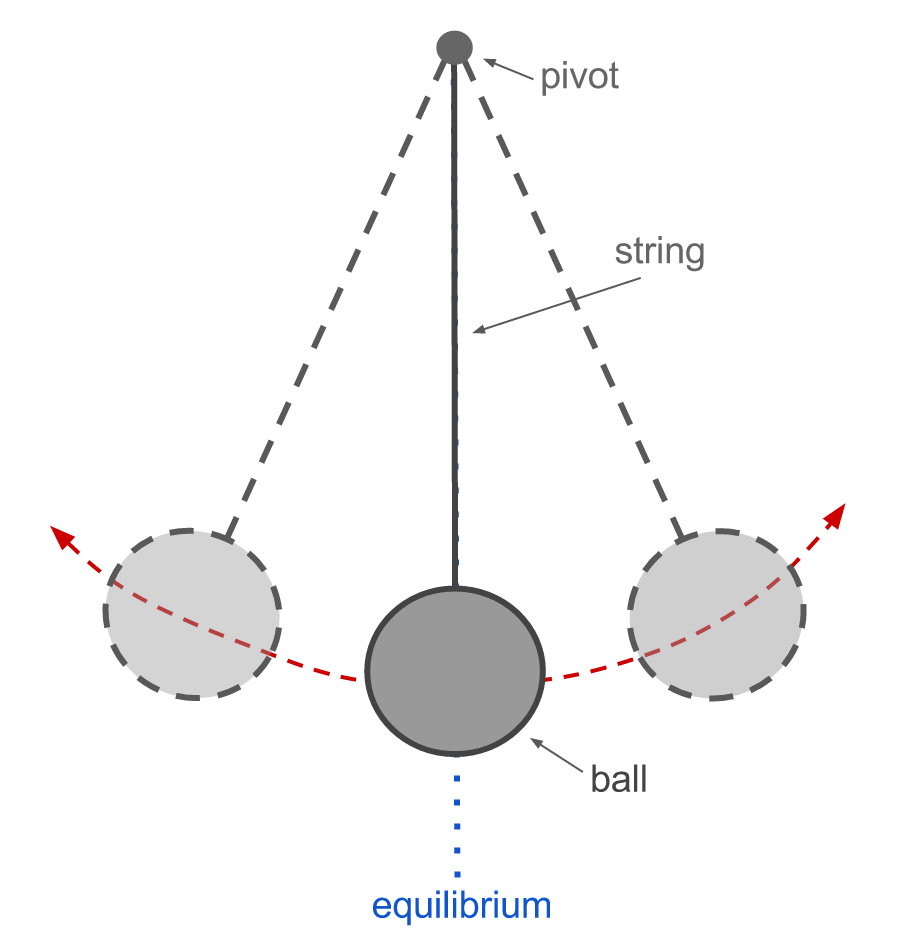
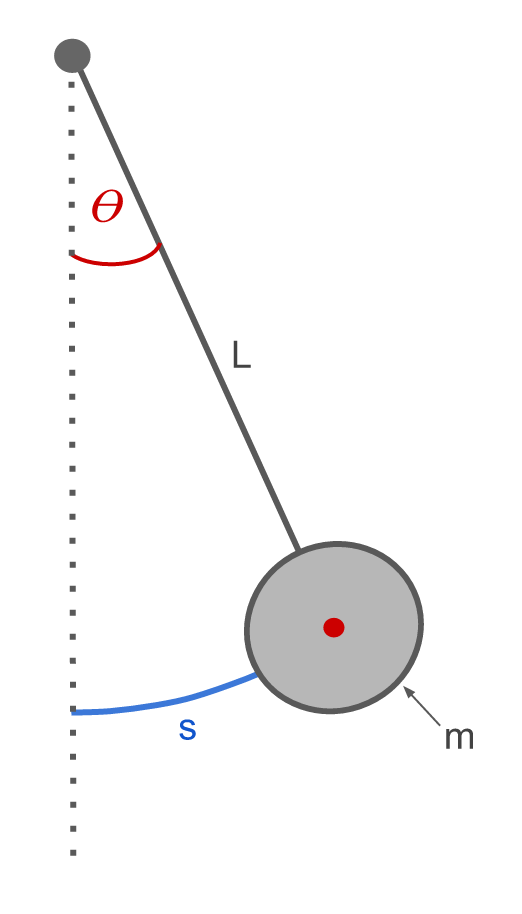
We will say that the string has length L and the ball suspended from it has mass m. For simplicity, we will assume that the pivot is frictionless and the string is massless. The displacement of the pendulum from equilibrium can be described by an angle θ and an arc-length s. Both of these parameters are 0 when the pendulum is at the equilibrium position.

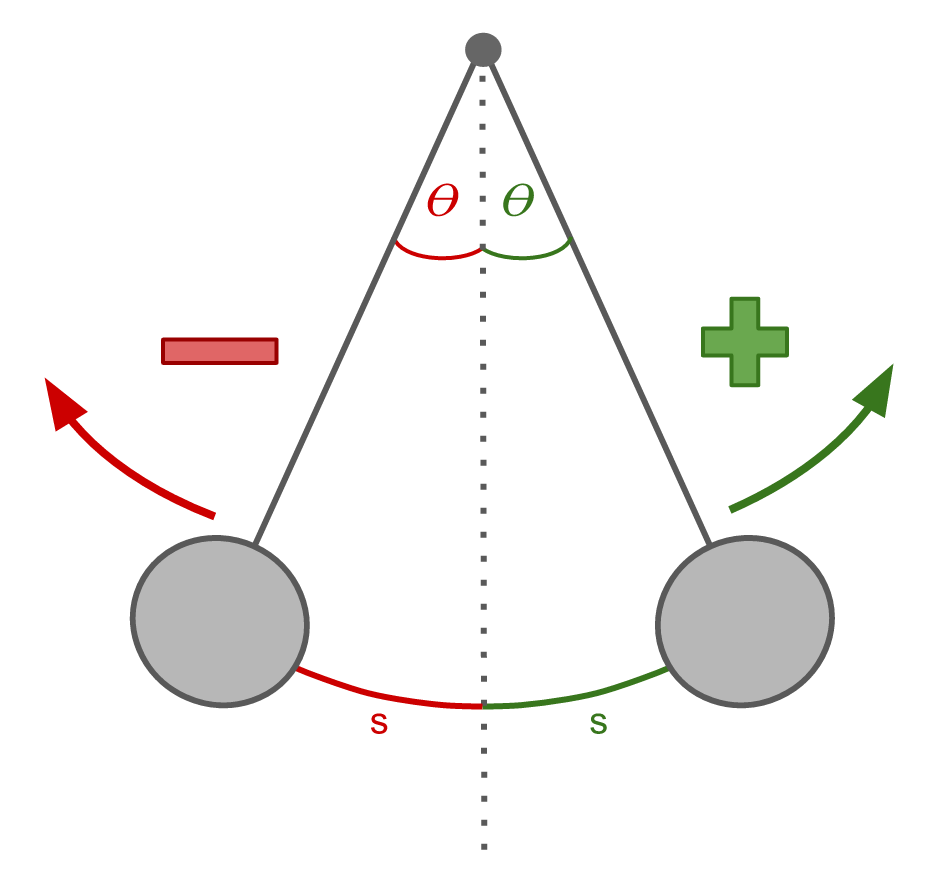
By convention, angles are measured such that counterclockwise is positive and clockwise is negative. When the pendulum swings to the right, both θ  and s are positive, while they are both negative when the pendulum swings to the left.

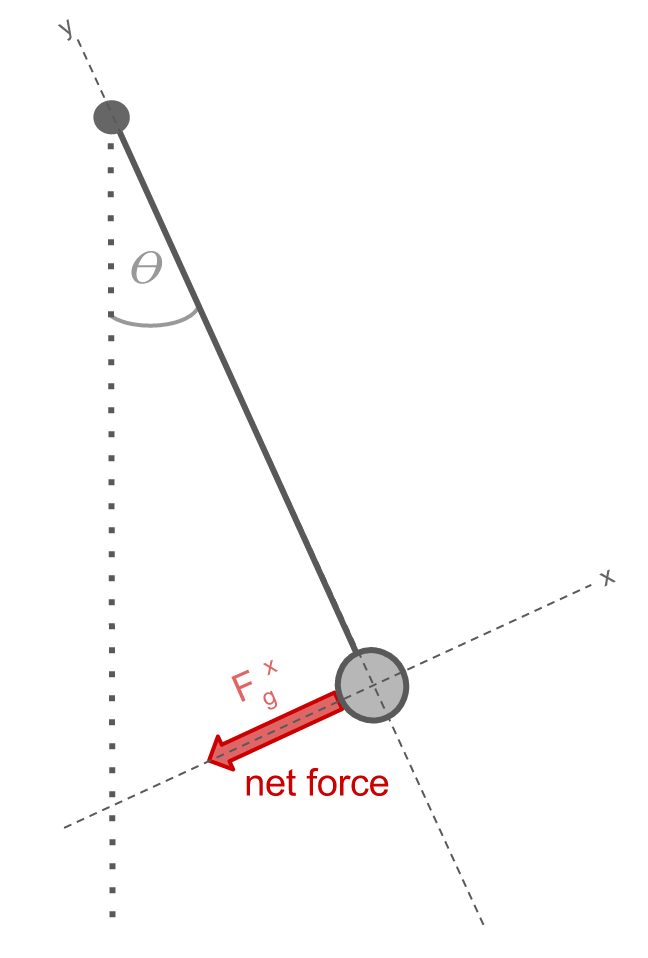
We can construct a free-body diagram to examine the forces acting on the pendulum mid-swing:

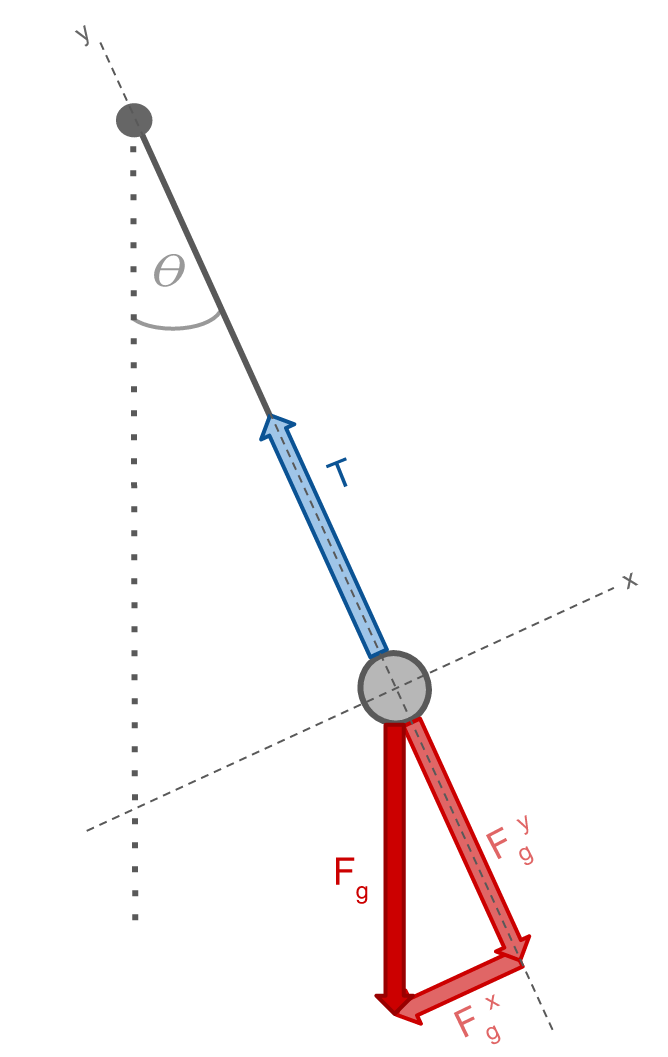
We can define the axes to be such that the y-axis lies along the string and the x-axis is perpendicular to it. The string provides a tension force (T) on the ball, which acts in the positive y-direction. The only other force acting on the ball is the force of gravity (F_g). This force acts in the downward direction, and can be broken up into its x- and y-components (F_g^x and F_g^y). Since F_g^y and T are of equal magnitude and directed in opposite directions, those forces cancel one another so there is no net force in the y-direction. The net force thus consists only of F_g^x:

The force of gravity is expressed as:

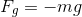
so the x-component can be written as:

Newton’s second law is: 

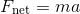
so our equation of motion for the pendulum is thus:

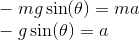
Writing acceleration as the second derivative of distance (s), this becomes:

------------------------------------------------------------

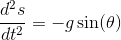
The pendulum moves a distance along an arc length (s) of a circle with radius r:

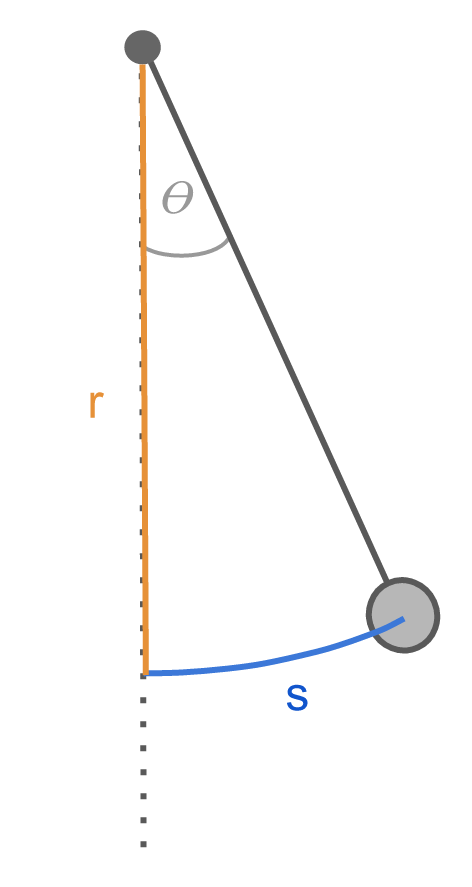
We can express the arc length as:

where θ is in radians.

------------------------------------------------------------

To simplify the equation of motion, we can implement the small-angle approximation, which holds for angles less than ~10°. We can look at the right-angle triangle created by the ball with the equilibrium position, denoting the horizontal distance from the ball to the equilibrium as h. Since this is a right-angle triangle, we can trigonometrically express h as:

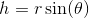
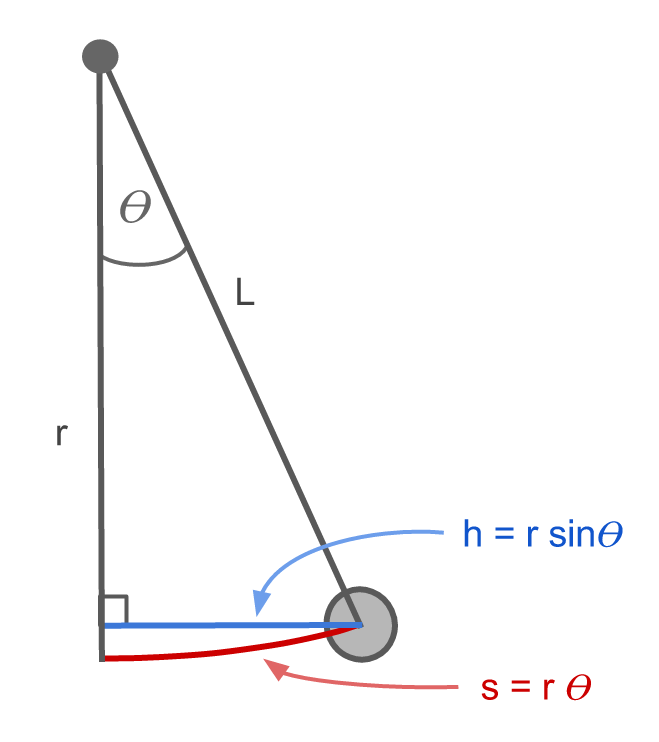
If θ is small, the lengths of h and s will be approximately the same: 

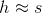
and therefore:

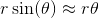
which gives rise to the small angle approximation:

where θ is in radians.

From this it follows that:

------------------------------------------------------------

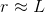
Using the small angle approximation, we can simplify our equation of motion to:

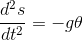
Replacing θ using the definition of arc length (s = r θ) and using the approximation that r ~ L, our equation becomes:

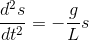
This is a second-order differential equation, for which the solution is:

where A is the amplitude of the oscillation and φ₀ the phase, both of which are set by the initial conditions of the pendulum. The angular frequency, ω, is defined as:

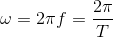
where f is the frequency and T the period. This solution yields an angular frequency of:

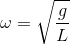
for the pendulum. The period and frequency of the pendulum do NOT depend on the mass of the pendulum, they depend ONLY on the length of the string. A 1 gram pendulum will have the same period as a 100 kg pendulum so long as the strings are the same length.

Rearranging the above equations, we see that the the period of a pendulum (that is, the time to complete one full swing back and forth) is given by:

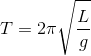which depends only on the length of the string.

Apparatus:

• two pendulums of different masses (cork and metal balls were used here), with adjustable length strings
• stopwatch
• metre stick

Procedure:

• hang two pendulums of different masses from strings the same length (after measuring with metre stick)
• using the stopwatch, measure the period of each pendulum and note that they are the same, independent of their mass
• change the length of the string of one of the pendulums and note how the period changes