How Does a Tippe Top Work?

When spun fast enough, a tippe top will flip over!

Watch The Video:

Levitron	Bicycle Wheel Gyroscope	How to Make a Tower of Lire

Teachable Topics:

• rotational motion
• angular momentum
• precession

Theory:

Before we investigate how the tippe top works, let’s first look at the mechanics of a regular spinning top:

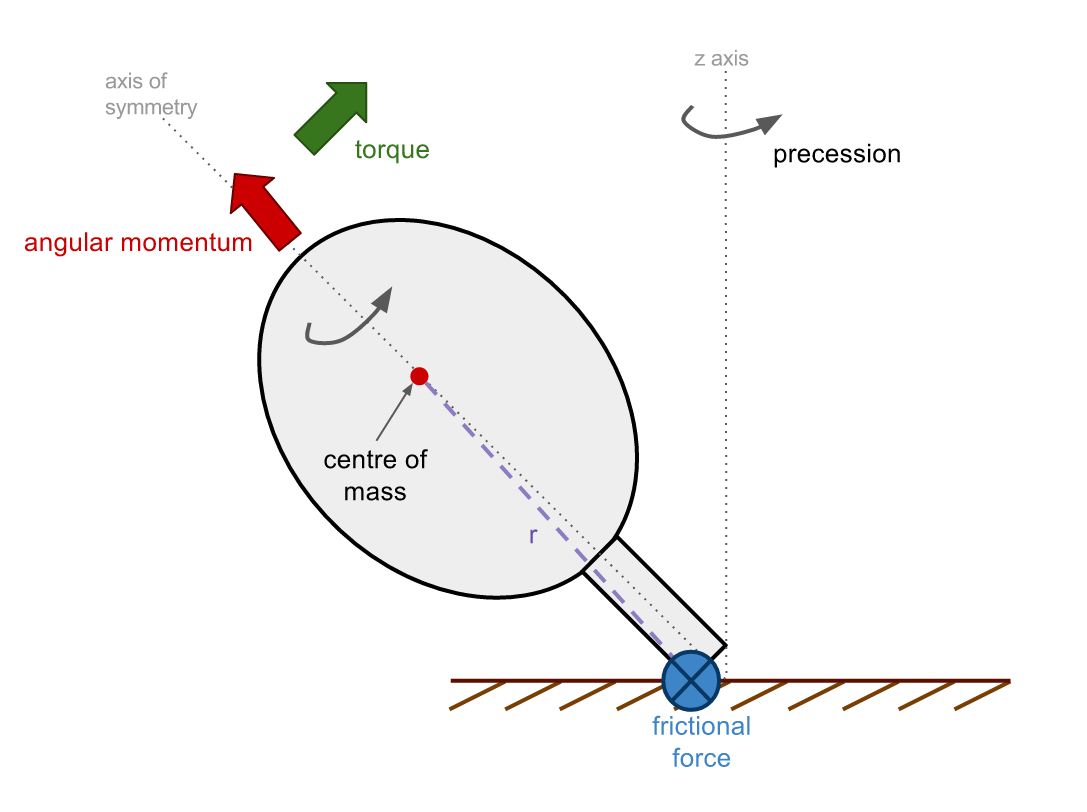
A regular top spins about its axis of symmetry, so the angular momentum is primarily directed along this axis (red arrow). 

The top provides a frictional force on the table which produces a torque about the centre of mass (green arrow). The torque, T,  is perpendicular to r, and will align the angular momentum with the z-axis, thus the top precesses (wobbles) about the z-axis normal to the table.

T = r x F

where r is the vector between the force and the centre of mass, and F is the frictional force.

The major difference between a regular top and a tippe top is the direction of the angular momentum - it is this distinction which accounts for the curious behaviour of the tippe top.

Unlike the regular top, for which the angular momentum is directed primarily along the axis of symmetry, the angular momentum of the tippe top always lies predominantly on the z-axis (red arrow):

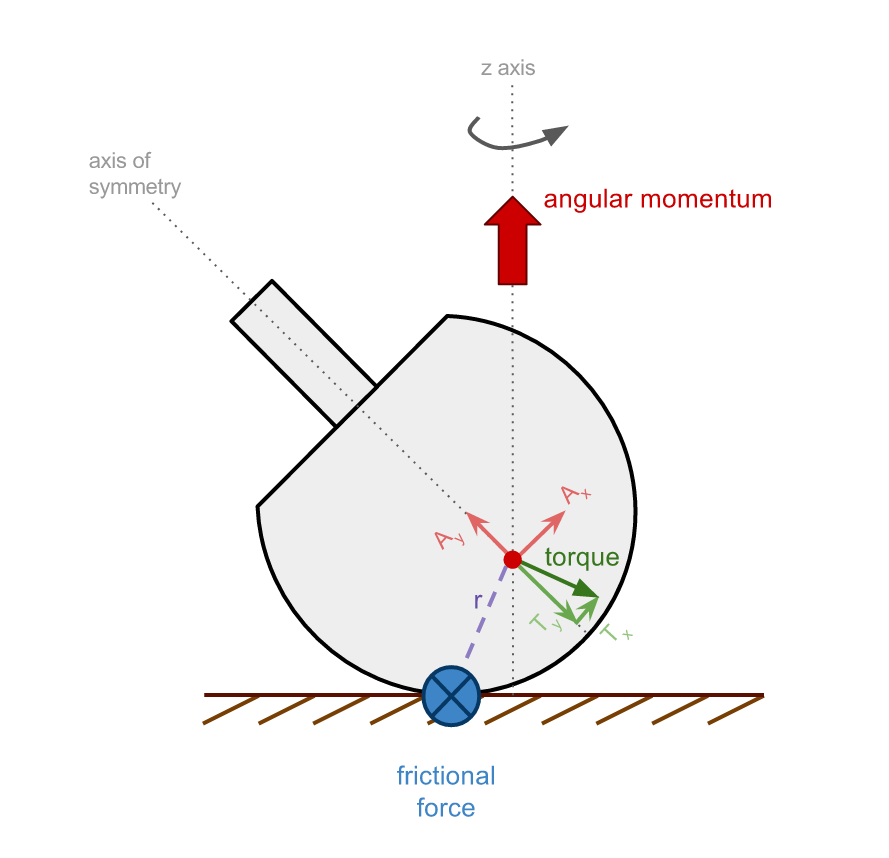
We can treat this angular momentum as a vector and break it down into two components: A_x and A_y (light red arrows). A_y is parallel to the axis of symmetry of the tippe top while A_x is perpendicular to it. Together, these components make up the total angular momentum.  

Just as in the case of the regular spinning top, the tippe top exerts a frictional force on the table. This force produces a torque on the tippe top which is perpendicular to r (dark green arrow).

Like the angular momentum, this torque can be broken down into its vector components (light green arrows), with T_y parallel to the axis of symmetry and T_x perpendicular.

These torque vectors will affect the angular momentum vectors. T_y opposes A_y, so the torque will decrease the angular momentum along that axis. T_x and A_x point in the same direction, so the torque will increase the angular momentum in that direction.

However, the total angular momentum (dark red arrow) must remain directed along the z-axis, so to ensure that the components A_x and Ay add up to the total angular momentum, the tippe top must rotate to preserve angular momentum.

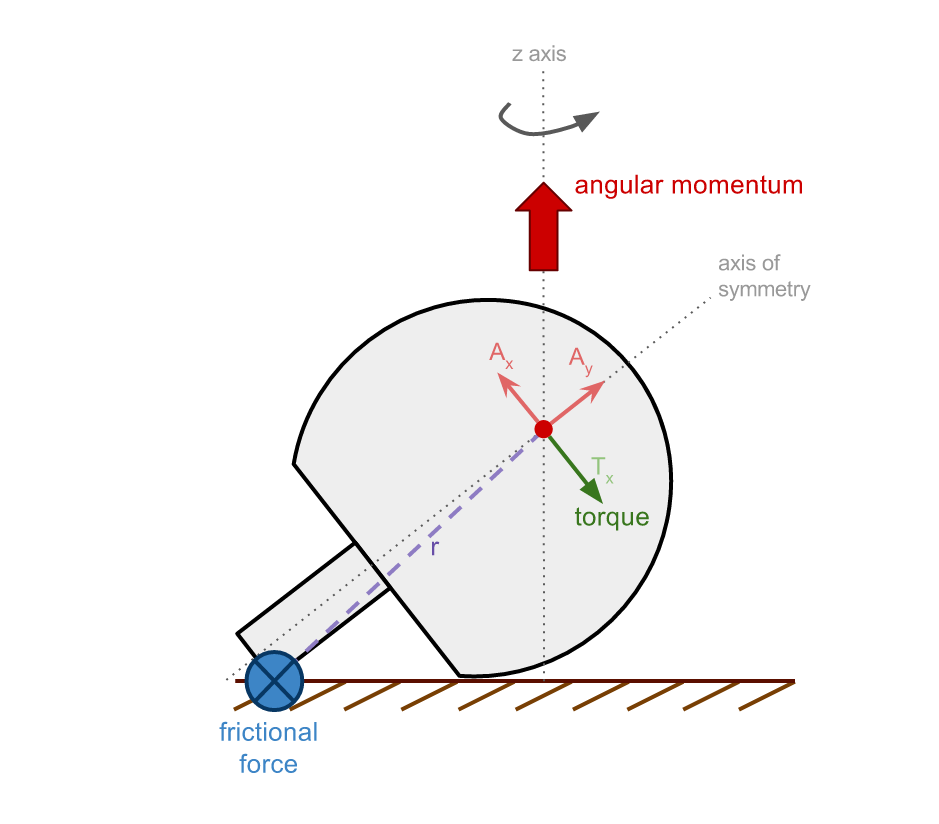
When the tippe top has rotated 90° from the vertical, the only component of angular momentum is along the z-axis (A_x). As always, the torque produced by the frictional force is perpendicular to r. Breaking this torque into its components shows that T_x opposes A_x thus reducing the total angular momentum.

Once the tippe top has rotated such that the stem touches the table, the frictional force then originates from the bottom of the stem. The torque produced from frictional force (again proportional to r) opposes the angular momentum component A_x so to maintain total angular velocity along the z-axis (and satisfy vector addition), the the tippe top must rotate to further align A_y with the z-axis.

When the tippe top has fully inverted, the axis of symmetry is aligned with the z axis, and so the angular momentum consists entirely of the A_y component:

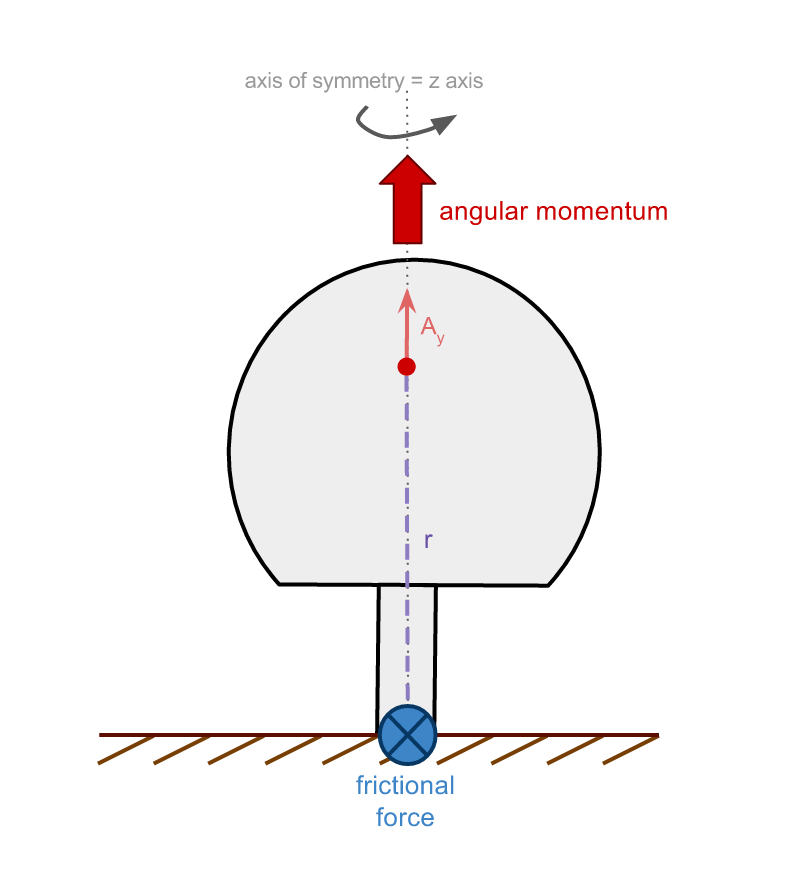
When the top inverts, the total angular momentum decreases. This means that the kinetic energy of the tippe top also decreases, thus increasing the potential energy. This increase in potential energy goes into raising the centre of mass (red dot):

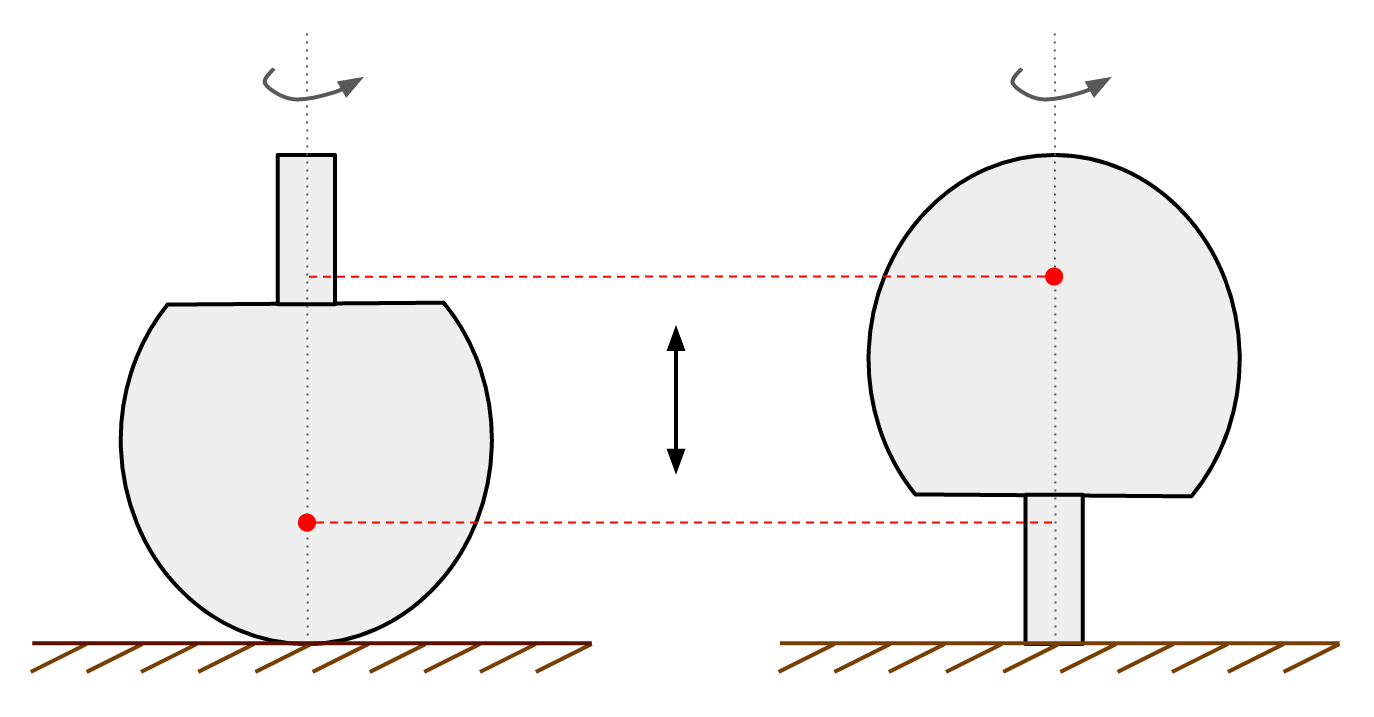
So in order for a successful flip to occur, the tippe top must be spun with a large enough initial velocity such that after losing angular velocity and angular momentum (and gaining potential energy) the top can remain spinning on its stem. 

Apparatus:

• a tippe top

Procedure:

• Holding the stem, spin the tippe top on its body
• Watch as the tippe top flips itself over while spinning to balance on its stem!

Tips: We recommend you practice this demo before you try to show it to anyone. It can take a few tries before you figure out the necessary speed required to spin the apparatus.