The force table illustrates the vector addition of forces.
Watch The Video:
Teachable Topics:
- Static equilibrium
- Acceleration
- Free Body Diagrams
Theory:
If an object is in static equilibrium, it is in an unchanging state. Newton’s 2nd law tells us that F = ma; a net force F acting on an object of mass m will cause the object to accelerate at a. If an object is accelerating, then clearly it is not in an unchanging state! Hence one of the conditions for static equilibrium is that there can be no net force acting on an object, otherwise it will accelerate. Of course, that does not mean that there can be no forces at all acting on an object - static equilibrium only requires that the vector sum of all the individual forces must add up to zero,
∑F = 0
In other words, the resultant force must be zero when several individual forces are exerted on an object. Because force is a vector, we must consider x, y, andz vector components separately. The true condition for static equilibrium is that
∑Fx = 0 ; ∑Fy = 0 ; ∑Fz = 0
Consider the simple example shown below. Two ropes are pulling on an object, each with the same force, but in opposite directions. We know from everyday experience that the force from the two ropes will cancel each other out, and hence the object won’t move - this is an example of static equilibrium.
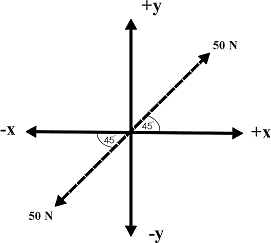
You can show that the condition for static equilibrium is satisfied for both the xand y directions. For example, in the x direction,
∑Fx = (50 N)(cos45°) - (50 N)(cos45°) = 0
where the difference in the + and - signs is because the force on the right is pulling in the +x direction and the force on the left is pulling in the -x direction. If you do the same thing for the y direction you will also find that [SUM] Fy = 0. Since there is no net force here, the condition for static equilibrium is fulfilled.
Apparatus:
- Force Table
- Various Weights
- Mass Balance
Procedure:
Forces are applied to the small ring on the force table by strings, to which different weights can be attached. The total force on a string is simply the weight of the masses hanging off the end plus the weight of the hanger itself. Hence,
Fon string = mhanger g + mweights
where g = 9.81 m/s2is the acceleration due to gravity on Earth. Note that the magnitude of the force on each string can be changed byadding or removing different weights, and the direction of the force can be changed by moving the arms on the force machine.
The pin at the centre serves as a reference point for centering the ring and also prevents the ring from falling off the table in highly unbalanced situations.
Using three strings instead of four is a simpler way to do this experiment, so remove one of the four hangers. The three strings should initially be about symmetrical. Make sure that the strings are centred properly on the ring (i.e. slide the knots so that the strings aren't twisted around the ring). Then load the three hangers with three different amounts of weight (note: try to use pretty heavy weights; the experiment works better then).
Most likely you will find that the ring will not be centred. That means that it is not in static equilibrium - if the forces from the three strings exactly balanced, then the ring would be perfectly centred on the table. Instead, it is being pulled to one side or the other because it is feeling a net force; if the central pin weren't there, the ring would accelerate right off the end of the force table in accordance with Newton's second law
 Figure 1: Labelled Force Table
Figure 1: Labelled Force Table
Move the strings until the ring is free of the pin and nearly centred. Gently tap on the force table to temporarily eliminate friction, which will allow the ring to move more freely to its new position. Re-adjust the positions of the strings and repeat the tapping until the ring is well-centred and remains there. The ring is now in static equilibrium, since the vector components of all three forces cancel one another out - there is no net force acting on the ring.
Record the total weight on each hanger (including the hanger itself) and the direction of each string, which is the angle written on the force table. Be sure to number each string and its corresponding weight and angle. Make a sketch of your force table.



