A Look at Center of Oscillation

Two physical pendulums rotate about different centres but have the same period of oscillation.

Watch the Video:

• Moment of Inertia
• Center of Oscillation
• Physical Pendulums

Theory:

In this experiment, the swinging rods are behaving like a physical pendulum. A physical pendulum is an object free to rotate about a pivot point, labeled O. For these kinds of pendulums, the period is:

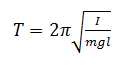
where m is the mass of the physical pendulum, g is the acceleration due to gravity, l is the distance from the centre of mass to the point of rotation O, and I is the moment of inertia. The moment of inertia is defined as the rotational inertia of an object relative to a fixed axis of rotation. Moment of inertia is given by the formula:

 I = mk²

where k is the radius of gyration. The value of k is different depending on the shape of the object rotating and where the axis of rotation is located. Substituting in this formula for the moment of inertia, the period of a physical pendulum becomes:

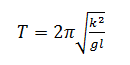
Using the parallel axis theorem, k can be expressed in terms of the radius of gyration around the centre of mass, k_{cm .} The parallel axis theorem states that the moment of inertia of an object about any axis of rotation is equal to the moment of inertia around a parallel axis passing through the centre of mass plus the object's mass times the distance between the two axes squared. In other words:

 I = I_cm + ml ²

This can in turn become:

mk² = mk_cm² + ml ² 

And by dividing out the mass, m, we get: 

 k² = k_cm² + l ² 

This can now be substituted into the pendulum period equation to get:

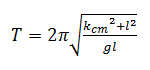
Now imagine that the axis of rotation was moved to a new point, O', a distance l' away from the centre of mass of the physical pendulum. The new period would be:

The periods of oscillation around O and O' would be the same given that:

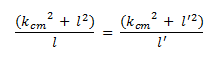
This reduces to:

 k_cm² = ll' 

For a rod of length a rotating about one end, k_cm²  is a²/12. Assuming the rod is uniform, the centre of mass will be located at the centre of the rod, a/2. Plugging these values into equation 6, we find that l' equals a/6.

This means that the rod will have the same period when swinging about a point located a distance a/6 away from the centre of mass as it will when it is swinging about one of its ends. Points O and O' are each others centre of oscillation.

In this experiment the rod is a meter long, thus O' is located at a point 100 cm / 6 = 16.67 cm away from the centre. 

Apparatus:

• Two uniform, identical rods, one meter long

Procedure:

1. Hang one rod from a support so that it will be able to swing back and forth like a regular pendulum. Hang it off the support such that it will rotate about one of its ends.
2. Hang the second rod from another support so that it too will swing like a pendulum. Hang this one so that it will rotate about a point that is about 16.67 cm away from the centre of the stick.
3. Place the two physical pendulums you created beside each other. Pull each rod back about the same distance and let go. Both rods should now be swinging back and forth with the same period of oscillation.