Kinetic Friction Demonstration

Kinetic friction slows a sliding block. 

Watch The Video:

Teachable Topics:

• Kinetic Friction
• Tension
• Inclined Planes

Theory:

Calculating the velocity of a block being pulled across a frictionless plane is a simple matter... but who ever heard of a frictionless plane?

Accounting for frictional forces is one of the first steps in doing "real" physics. That is, taking into account the forces that act in non-ideal situations.

An example of such a non-ideal situation is a wooden block sliding across a wooden board. If the block is given a short push, it will slow down and eventually stop. It slows down because it is acted upon by a frictional force, f_k. If we wanted the block to keep moving, we would have to counteract the frictional force with another force. This new force could be created by attaching a string to the block, draping the string over a pulley, then attaching some weights at the other end of the string. A tension force, T, then acts on the block.

If it's strong enough, the pull of the string on the block, T, will keep the block moving after it is pushed (in spite of the friction from the board).

Figure 1: Labelled Diagram

The kind of friction discussed here is called kinetic friction. Kinetic friction is the force which opposes the motion of a sliding object. It depends on the normal force on the object and the kind of materials that make up the object and the surface. The formula for this force is

f_k = υ_kN

The setup described above, where the moving block is kept in motion by the string and the weights, is a simple way to measure the coefficient of kinetic friction. If just the right weight, Mg, is added to the end of the string to keep the block moving at a constant speed, then the net force on the block must be zero (if it weren't, the block would speed up or slow down)

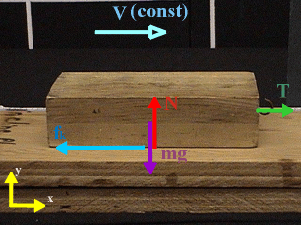
Figure 2: Forces acting on/by the block

The sum of all the forces in the x-direction is ∑F_x = T - f_k=0 and therefore, T = f_k = υ_kN, as given above.

Since the tension in the string. T, is equal to Mg (where M the mass of the weights hanging at the end of the string), we have T = Mg = υ_kN

The sum of the forces in the y-direction is ∑F_y = N - mg = 0, and therefore, N=mg.

Combining this with the equation above, we get: Mg = υ_kmg or M/m = υ_k.

That is to say, the coefficient of kinetic friction is the mass of weights divided by the mass of the block!

Apparatus:

• Wooden block
• Weights
• Pulley
• String

Procedure:

• Push the block across the surface. The block will slow down once shoved because of kinetic friction.
• For the next part, place weights at the end of a string, which is attached to the block.
• Give the block a push to start it. If the block slows to a stop, add more weights until the block slides at a constant velocity.