Ever want to hear or see beat frequencies? Here you go!
WATCH THE VIDEOS
Hearing Beats
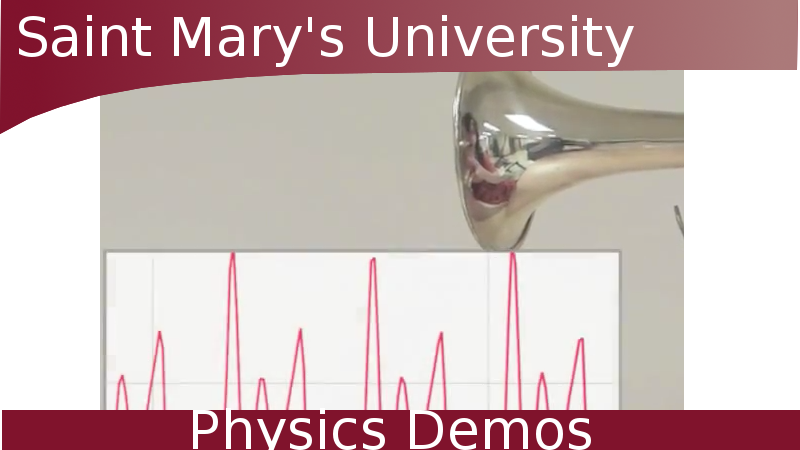
Seeing Beats
 |
 |
 |
|
What Does Music Look Like |
Standing Waves and Strobe |
Wave Interference |
- Sound and Music
- Frequencies
- Interference
Theory:
Beat frequencies occur when the waves from two waves sources, each with different frequencies, interfere with each other. This produces a single tone whose volume oscillates between loud and soft. This tone that is constantly changing volume is what is referred to a beats.
In order to find these beats, consider two waves interfering. Assume their amplitudes are the same and that there is no phase difference. Thus the waves can be expressed as:
x1 = A cos (ω1t)
x2 = A cos (ω2t)
where A is the amplitude, ω is the angular frequency, t is time, and the subscripts 1 and 2 are used to differentiate between the two waves. Add the two waves together:
x = x1 + x2
x = A cos(ω1t) + A cos(ω2t)
x = A [cos(ω1t) + cos(ω2t)]
To simplify, use the trig identity:
cos α + cos β = 2 cos[(α - β) / 2] cos[(α + β) / 2]
Thus we get:
x = 2A cos[(ω1 - ω2)t / 2] cos[(ω1 + ω2)t / 2]
If we let (ω1 + ω2) / 2 = ωavg (the average angular frequency) and let (ω1 - ω2) / 2 = ωmod (the modulation frequency), we can simplify to:
x = 2A cos(ωmodt) cos(ωavgt)
This formula for the addition of two waves is true for any values of ω1 and ω2, but for beat frequencies we are looking at a certain case. For beat frequencies to occur, the two angular frequencies must be close in value. In other words:
|ω1 - ω2| << ω1 + ω2
This means that ωavg is similar in value to ω1 or ω2, while ωmod is very small, close to zero. This means that the cos(ωmodt) term is oscillating very slowly. Together with the 2A term, 2A cos(ωmodt) provides the slowly changing amplitude for the cos(ωavgt) function.
As it turns out, the beat frequency is twice the modulation frequency, fmod. fmod is equal to ωmod divided by 2π. Thus:
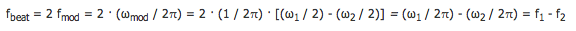
where f1 and f2 are the frequencies of the two waves sources. Thus, the beat frequency is just the difference in the frequencies of the two wave sources.
Apparatus:
- Hearing Beats: Two tuning forks of different (but close) frequencies. In the video a tuning fork of 250 Hz and one of 238 Hz were used.
- Seeing Beats: Two tunable speakers and an oscilloscope attached to a microphone
Procedure:
- Set up the two tuning forks near each other and strike them one at a time.
- Listen for the beat frequency. It will be a single tone that is alternating between being loud and soft.
- Use an oscilloscope to "see" the beats



