The connection between simple harmonic and circular motion.
Watch The Video:
Teachable Topics:
- uniform circular motion
- simple harmonic oscillator
Theory:
Consider an object in uniform circular motion along a path of radius A. The object starts at an angle Θ = φ at time t = 0 and begins to move with angular velocity ω. After time t has elapsed, the angular position of the object is:
Θ = φ + ωt
We've just described the motion of the particle as seen from above, but what would a person see if that person viewed the object's motion side-on?
To describe what this person sees, we'll project the position of the object on to some diameter of its circular path. For simplicity, lets choose the x-axis. Using simple trigonometry, we can see that the x-projection is just
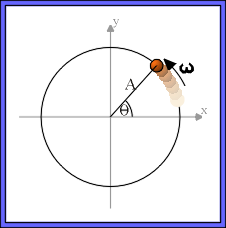
Figure 1: Uniform Circular Motion
Any motion which repeats itself is called harmonic motion, and when the equation of motion is of the form:
x = Acos(ωt + φ)
then it is called simple harmonic motion.
It is easy to see that the equation of the "side-view projection" of uniform circular motion and the equation for simple harmonic motion are identical. This implies that, seen end-on, uniform circular motion looks just like simple harmonic motion.
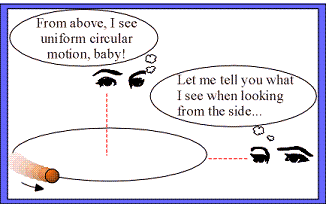
Figure 2: Point of view
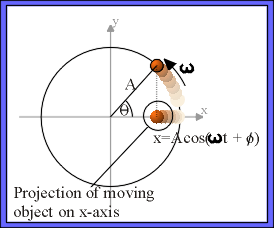
Figure 3: Coordinate transform
Apparatus:
- Cenco rotator
- weights
- spring and support
Procedure:
- Hang a spring from a support and attach several heavy masses to the end of the spring. You'll want a lot of mass on the spring so that it is stretched a lot. A spring which is stretched a lot can have a larger amplitude of longitudinal oscillation.
- Test the spring to make sure that the amplitude of oscillation is about the same distance as the diameter of rotation of the Cenco rotator.
- Now adjust the height of the support so that the equilibrium position of the masses on the spring is at the same height as the axis of rotation of the Cenco rotator.
- Turn on the rotator and stretch the spring so it begins oscillating.
- Carefully adjust the period of rotation of the rotator until it matches that of the spring.
- View the rotator from the side to see how its motion viewed side-on is similar to that of the spring.
You can use a light to project the shadows of the moving objects on a wall to make it easier to compare the motions.
Tips:
- When attempting to match the period of the rotator to that of the spring, have patience: this takes some time to master.



