When two waves overlap, the resulting wave is the sum of the two original waves.
Watch The Videos:
Destructive Interference
Constructive Interference
Teachable Topics:
- Superposition
- Waves
- Interference
Theory:
A wave is a moving disturbance in some medium. In a guitar string, the disturbance is the deviation of the string from its equilibrium position. In a sound wave, it is an increase or decrease in the pressure of the air. The wave machine is many bars lying horizontally. A disturbance causes the bars to be inclined or to be lowered.
If two waves are traveling toward each other, they will eventually meet. When they do, the resulting disturbance is the sum of the two original disturbances. This is the principle of superposition.

Figure 1

Figure 2
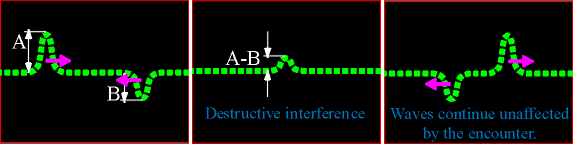
Figure 3
To clarify this principle, take the example where two crests travel toward one another and meet. One crest initially has a height A while the other has a height B. When the centres of the two waves exactly overlap, the height of the resultant wave will be the sum A + B. When this happens, it is called constructive interference.
Destructive interference occurs when a crest meets a trough. A crest with height A whose centre exactly overlaps the centre of a trough with depth B will result in a wave with height A - B.
After interfering with one another, the two waves travel on with their original shapes as if they had never met in the first place.
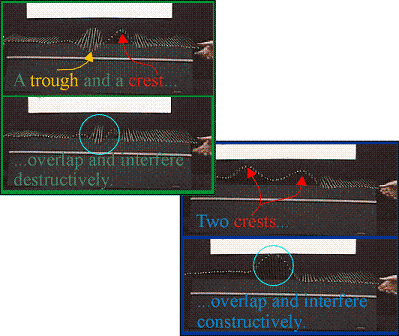
Here are photos taken from the videos below. They show the interfering waves just before and just after they overlap.
Apparatus:
- The large wave machine
Procedure:
- Set the large wave machine on a flat surface.
- Simultaneously create a crest on either side of the wave machine. As the waves come together, they will combine to form a wave larger than either of the individual waves.
- To show deconstructive interference, form a trough at one end of the wave machine and a crest at the other. Once the trough and crest meet, they will cancel one another out... that is, the resultant wave is smaller than either of the individual waves alone.



