Non-Isotropic Oscillator

This two dimensional oscillator makes Lissajous figures!

Watch The Video: 

• Lissajous Figures
• Motion of a Particle
• Non-isotropic Oscillators

Theory:

Consider the motion of an object subjected to a linear restoring force that is always directed towards the origin of the coordinate system. The restoring force is represented by the equation: 

F = -kr

Or:

mr'' = -kr

For a multidimensional oscillator where the spring constants are not all the same, we have a non-isotropic oscillator. In this case, the motion can be represented by the component equations:

mx'' = -k₁x

my'' = -k₂y

where k₁ and k₂ represent the different spring constants. In this case, there are two different frequencies of oscillation, ω_x = (k₁ / m)^1/2 and ω_y = (k₂ / m)^1/2. Solving the equations, the motion of the object is described by:

x = A cos(ω_xt + α)

y = B cos(ω_yt + β)

The constants of integration (A, B, α, β) are all determined by the initial conditions. For the most part, the object will follow a semi-chaotic path. However, for the case where ω_x and ω_y are commensurate:

ω_x / n₁ = ω_y / n₂ 

where n₁ and n₂ are some arbitrary integers, the object will follow a closed loop known as a Lissajous figure. The object will go around this loop, and after a certain amount of time, the object will return to its initial position and then repeat its path.

In the video above, the Lissajous figure is similar to a figure eight with half of one loop removed. The path the air puck traces out looks like:

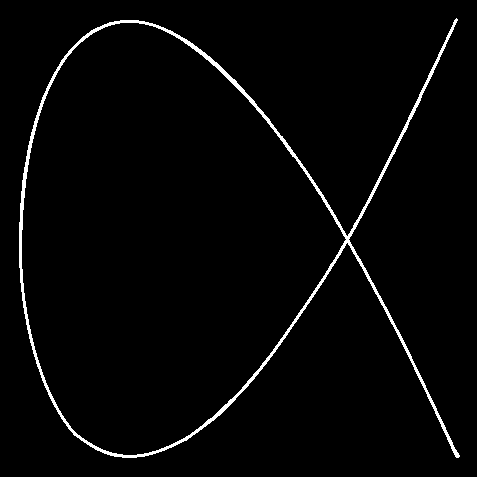
_{Figure 1: 3:2 Ratio Lissajous Figure} 

 The air puck will follow this path when the phase difference is π / 2, and the ratio of frequencies is 3:2 (as in 3ω_x = 2ω_y).

Apparatus:

• Air table with air supply
• Air puck with hooks for springs
• Four springs (Note: The springs should be in two pairs, one pair for the x-direction and one pair for the y-direction. The spring constant of each pair must be so that ω_x and ω_y are commensurate.)
• Four clamps and supports for them.

_{Figure 2: Apparatus Set-up (viewed from above)} 

Procedure:

• Assemble the apparatus, referring to figure 2 and the video.
• Pull the puck in one direction and let go. Observe the Lissajous figure that is traced out by the air puck.