Hearing and Visualizing Beat Frequencies

Ever want to hear or see beat frequencies? Here you go! 

WATCH THE VIDEOS

Hearing Beats 

 Seeing Beats

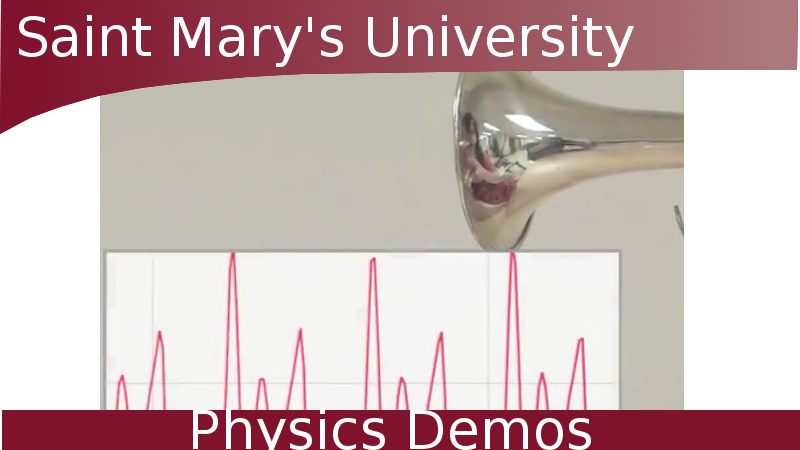What Does Music Look Like	Standing Waves and Strobe	Wave Interference

• Sound and Music
• Frequencies
• Interference 

Theory:

Beat frequencies occur when the waves from two waves sources, each with different frequencies, interfere with each other. This produces a single tone whose volume oscillates between loud and soft. This tone that is constantly changing volume is what is referred to a beats.

In order to find these beats, consider two waves interfering. Assume their amplitudes are the same and that there is no phase difference. Thus the waves can be expressed as:

x₁ = A cos (ω₁t) 

x₂ = A cos (ω₂t)

where A is the amplitude, ω is the angular frequency, t is time, and the subscripts 1 and 2 are used to differentiate between the two waves. Add the two waves together:

x = x₁ + x₂

x = A cos(ω₁t) + A cos(ω₂t)

x = A [cos(ω₁t) + cos(ω₂t)]

To simplify, use the trig identity:

cos α + cos β = 2 cos[(α - β) / 2] cos[(α + β) / 2]

Thus we get:

x = 2A cos[(ω₁ - ω₂)t / 2] cos[(ω₁ + ω₂)t / 2]

If we let (ω₁ + ω₂) / 2 = ω_avg (the average angular frequency) and let (ω₁ - ω₂) / 2 = ω_mod (the modulation frequency), we can simplify to:

x = 2A cos(ω_modt) cos(ω_avgt)

This formula for the addition of two waves is true for any values of ω₁ and ω₂, but for beat frequencies we are looking at a certain case. For beat frequencies to occur, the two angular frequencies must be close in value. In other words:

|ω₁ - ω₂| << ω₁ + ω₂

This means that ω_avg is similar in value to ω₁ or ω₂, while ω_mod is very small, close to zero. This means that the cos(ω_modt) term is oscillating very slowly. Together with the 2A term, 2A cos(ω_modt) provides the slowly changing amplitude for the cos(ω_avgt) function.

As it turns out, the beat frequency is twice the modulation frequency, f_mod. f_mod is equal to ω_mod divided by 2π. Thus:

where f₁ and f₂ are the frequencies of the two waves sources. Thus, the beat frequency is just the difference in the frequencies of the two wave sources. 

Apparatus:

• Hearing Beats: Two tuning forks of different (but close) frequencies. In the video a tuning fork of 250 Hz and one of 238 Hz were used.
• Seeing Beats: Two tunable speakers and an oscilloscope attached to a microphone

Procedure:

1. Set up the two tuning forks near each other and strike them one at a time.
2. Listen for the beat frequency. It will be a single tone that is alternating between being loud and soft.
3. Use an oscilloscope to "see" the beats