A long chain turns into a fountain of self-siphoning beads!
 |
 |
 |
Levitron |
How a Tippe Top Works |
Peanuts on a Van der Graaf |
Teachable Topics:
- siphoning
- forces
Theory:
The physics behind the chain fountain is non-trivial. In fact, the entirety of the chain fountain effect is not yet entirely understood.
There are disputing theories as to why this phenomenon occurs which have not been reconciled into a universally agreed-upon explanation. Even so, prevailing theories lack a complete description of the mechanisms at play, resulting in an incomplete understanding of this curious phenomenon.
As such, we will examine two studies which have offered some analysis of this effect.
------------------------------------------------------------------------------------------------------------------------
In 2014, Biggins & Warner published a paper, “Understanding the chain fountain”, available here. (Video here.)
Their explanation of the chain fountain attributes this effect to an upward reactionary force from the pile of stationary chain in the beaker.
They model the chain as a series of rigid rods which are connected by free, flexible joints. The links are resting atop a rigid surface: the pile of chain below, or the beaker/table.
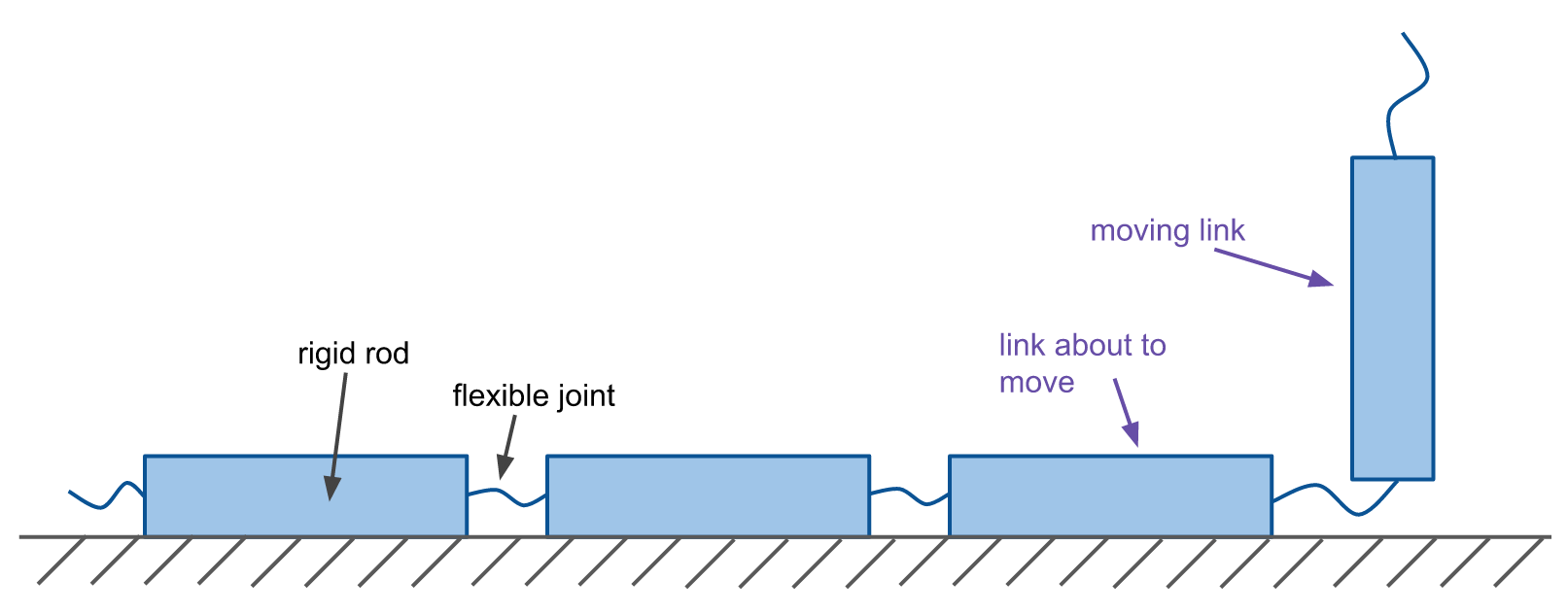
When a rod is pulled by a moving rod before it, the force acts on the end of the rod closest to the moving rod, not on the middle (where the centre of mass is).
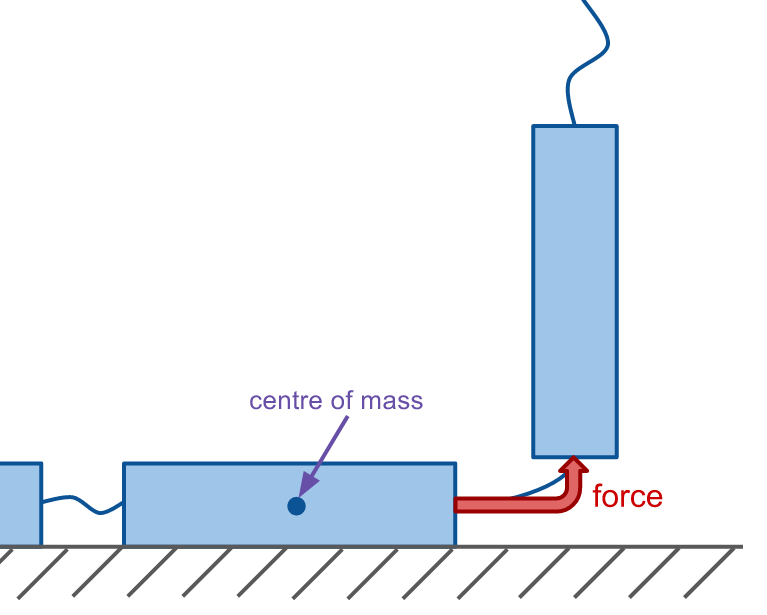
This upward force causes the rod to rise up higher, as well as rotate about its centre of mass:
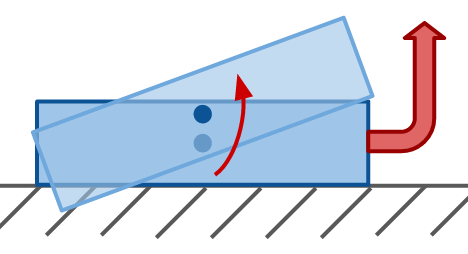
However, since the table (or pile of chain atop the table) restricts the rod from rotating into the table, it provides an additional upward force on the chain. Biggins & Warner argue that this upward force from the table is what causes the fountaining effect of the chain.
------------------------------------------------------------------------------------------------------------------------
The height of the beaker from the floor affects how high the fountain rises. The larger the distance is from the beaker to the floor, the higher the fountain is.
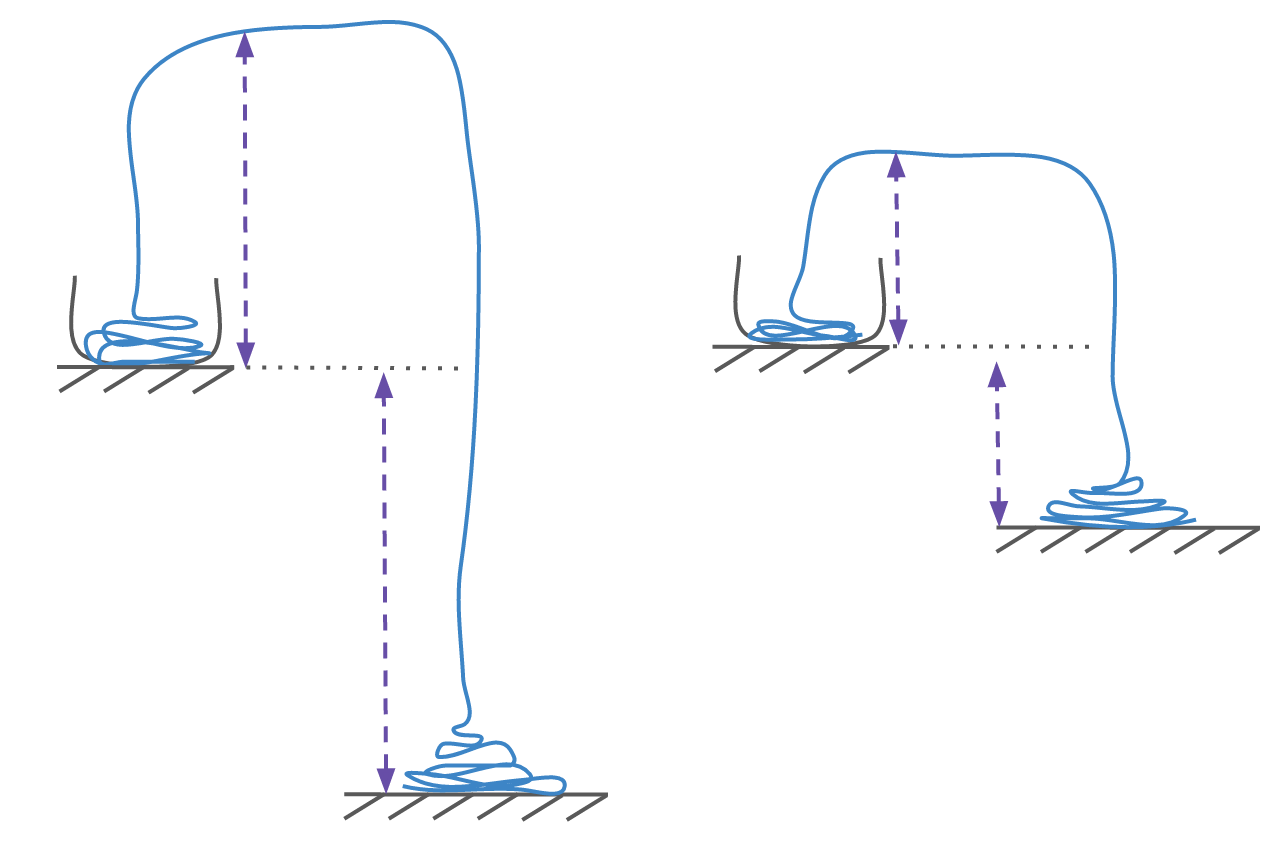
As the chain falls from the beaker to the floor, it releases gravitational potential energy. The weight of the chain that has left the beaker pulls the rest of the chain from the beaker. A larger gap between the beaker and the floor means the chain releases more gravitational potential energy, and so the chain travels faster.
Biggins & Warner argue that if the chain is falling a longer distance, it is moving faster, and a faster-moving chain means a larger upward force from the table when each link hits it. They say that a larger drop causes a greater force from the table which causes the fountain to rise higher.
------------------------------------------------------------------------------------------------------------------------
A 2016 paper by Rogério Martins, available here, further discusses the physics behind the chain fountain. He argues that the reactionary force proposed by Biggins & Warner contributes little to the chain fountain.
Martins found that the coiling of the chain inside the beaker affects the height of the fountain. The chain randomly filling the cup with many twists (top) produced a higher fountain than a neatly coiled chain (bottom). (Left diagrams are as seen from above.)
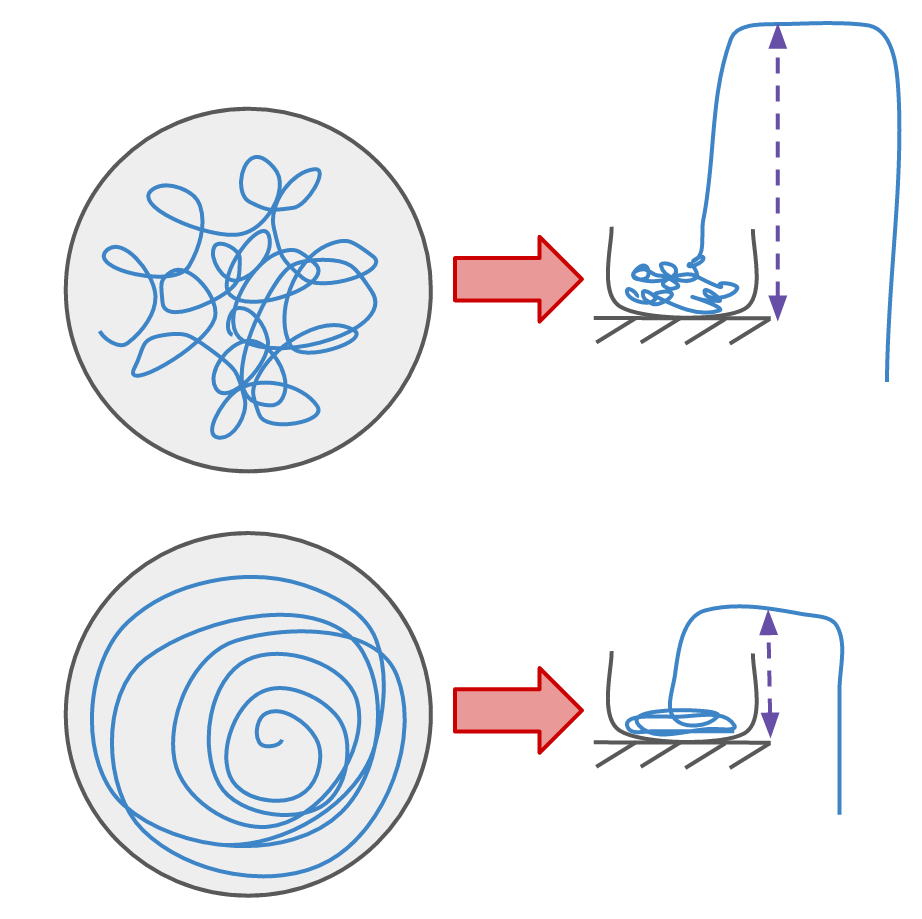
Since the fountain height depends on the configuration of the chain, the reactionary force postulated by Biggins & Warner is insufficient to explain this phenomenon, as the reactionary force is independent of chain configuration.
Martins’ work analysing video of chain behaviour frame-by-frame confirmed the presence of a reactionary force, though it also revealed additional mechanics at play.
Martins arranged a chain atop a table and hung one end off the edge of the table to simulate the configuration of the chain fountain. As viewed from above:
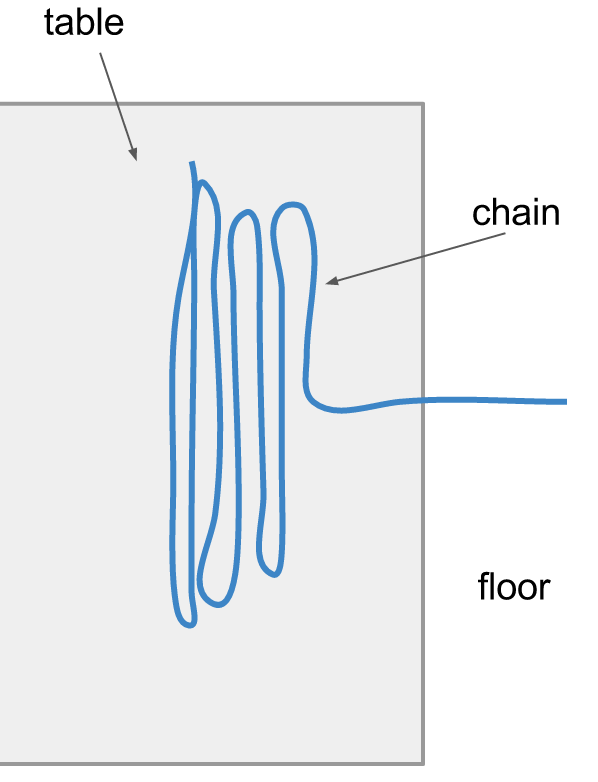
He found evidence of a reactionary force, but found that this force is not constant, occurring only at select points in the pile.
He also found that the chain exhibits a slight backlash before turning to fall to the floor:
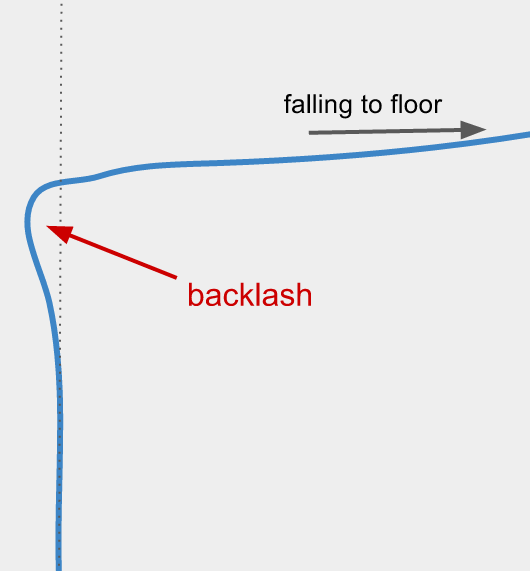
This was the phenomenon found by Martins most similar to the kick producing the reactionary force postulated by Biggins & Warner.
Martins attributes this backlash to a bound on the maximum possible curvature of a chain. As shown below, a segment of chain is only able to bend so much before the rigidity of the chain’s links prevents further curvature:
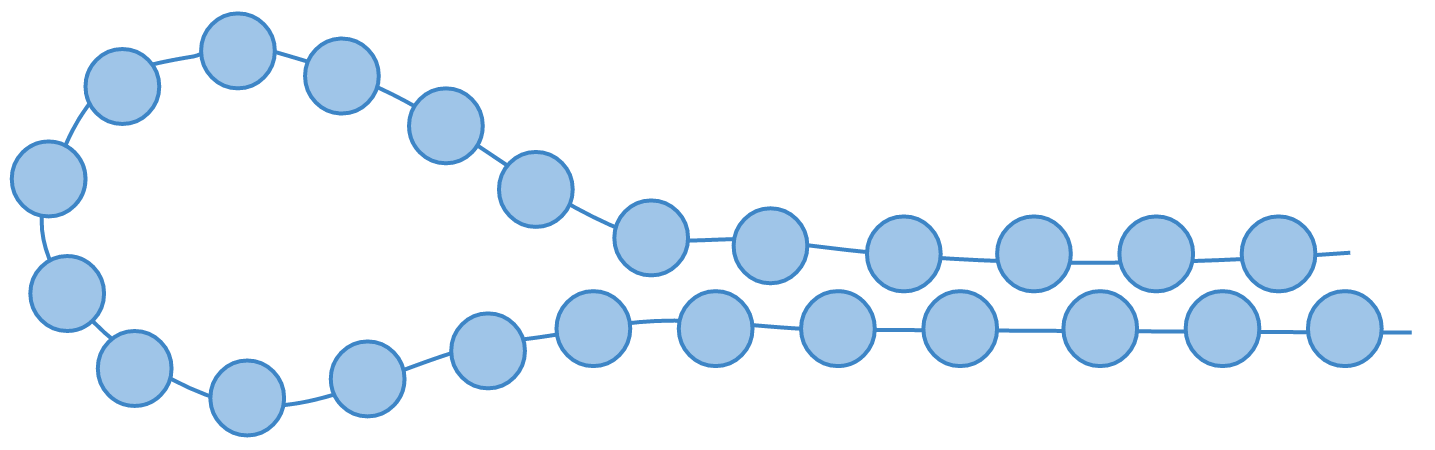
Martins found that there was additional backlash in the regions of the chain following a twist:
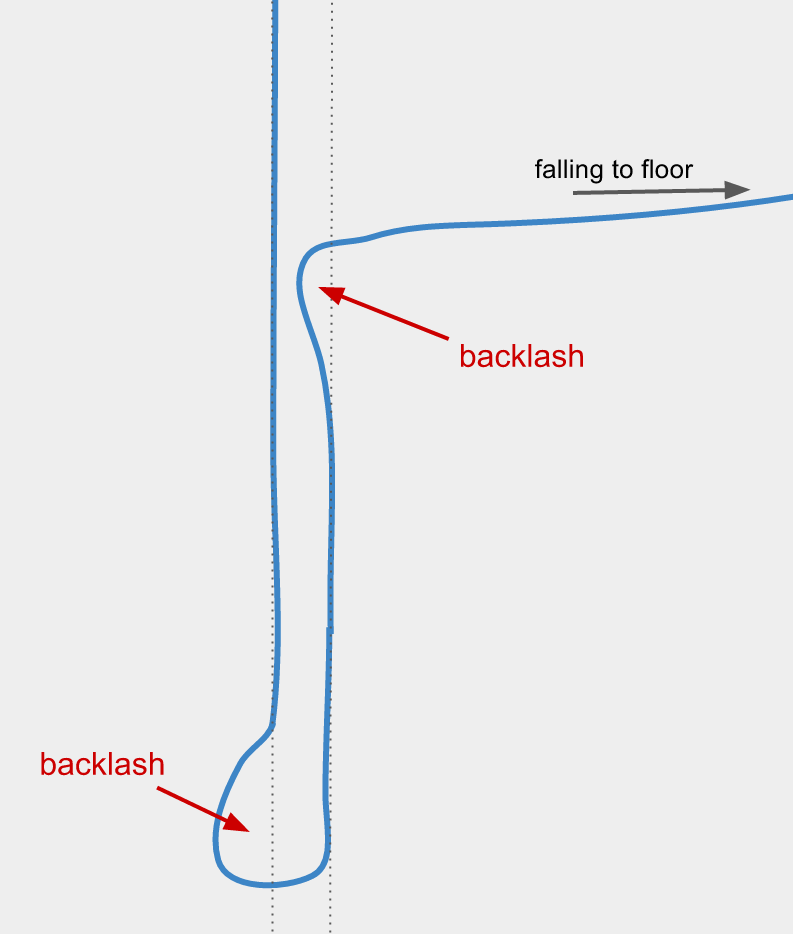
This backlash creates a free end of the chain, producing a whip effect.
Martins proposed that the chain fountain is a result of this backlash following twists in the chain. These backlashes produce a whip effect that push the chain, creating the fountain. This theory is able to account for the fact that more twists in the chain produces a higher fountain.
However, this theory is still incomplete, lacking a complete description of the mechanics of the chain fountain.
Apparatus:
- bathroom chain (100 feet long)
- beaker or container to hold chain
Procedure:
- pile chain in beaker, making sure not to tangle the chain
- pull the end of the chain over the edge of the beaker, towards the floor, and release



