This demonstration shows the pressure height gradient in a fluid.
Watch Video:
Possible Incorporated Topics:
- Pressure gradient
- Hydrostatic force
- Newton's Law
| Theory:
A sample of the water in a tank has a volume V = A(y1 - y2), where A is the top area of the sample, and y1 is the position of the top and y2 the position of the bottom of the sample. If the water has density r (Greek letter rho), then the weight of the sample is W = rgA(y1 - y2). Since the water is not flowing, then the total force on the sample must be zero. There must then be forces other than the weight acting on the sample. These other forces are the pressure on the top of the sample and the pressure on the bottom. If the pressure on the top and on the bottom are P1 and P2respectively, then the force on the bottom is F1 = P1A and the force on the top is F2 = P2A. Newton's Law give us the following relation.
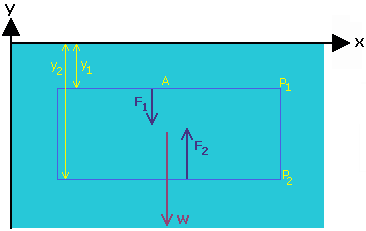 Figure 1: Forces acting within a tank of water |
P2A - P1A - rgA(y1 - y2) = 0
If we take P1 to be the pressure at the surface of the water, then it is equal to the atmospheric pressure: P1 = Patm and y1 = 0
If we make P2 to be the pressure at a depth of h below the surface, then:
P2 = P and y2 = -h
The bold equation from above thus gives us the following formula:
P = Patm + rgh
As this fomula shows, P increases with depth, h, in the fluid.
This result can be shown with a pipe filled with water. If the pipe has holes at a few different depths, then the higher pressure at the bottom forces the water out of the hole faster.
Apparatus:
- Clear pipe with three small holes
- Water supply
- Small tub or bucket
- Stand
- Tape
Procedure:
|
 Figure 2: Apparatus |



