Total internal reflection can be used to bend a beam of light.
WATCH VIDEO:
Other Demos of Interest:
Teachable Topics:
- Snell's Law
- Refraction
Theory:
Snell's law of reflection says that, for light passing from one medium (with index of refraction n1) into another medium (index n2) obeys the following relation:
n1 sin(q1) = n2 sin(q2)
where q1 is the angle of incidence and q2 is the angle of refraction. Rearranging this equation, we find
q2 = sin-1[(n1/n2)sin q1]
Now assume that n1 > n2 (this would be like having a beam of light in glass, n ~ 1.5 passing into air, n ~ 1, for example). We know that the argument of the inverse sine function must be between minus one and one. In this case,
-1 ≤ (n1/n2)sin q1 ≤ 1
∴ |sin(q1)| ≤ (n2/n1)
where n2/n1 is a fraction less than one. That is to say that there is a critical angle of incidence where q1 is given by sin(q1) = n2/n1. At angles of incidence greater than this one, Snell's law no longer applies.
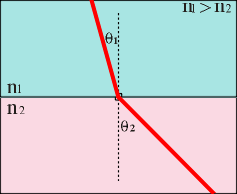
Figure 1: Snell's Law at the boundary between two substances
Experimentally, it is found that at angles greater than the critical angle, light is reflected back into the first medium. This effect is called total internal reflection, and can be demonstrated with a right equilateral triangular prism such as the one shown here (the sides are labelled for ease of referring to them later):

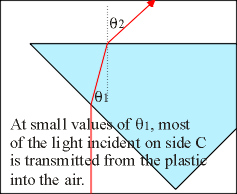
If a laser is shone into side A of the prism so that the light hits side C at a small angle of incidence, then most of the laser light is transmitted through side C and into the air around the prism.
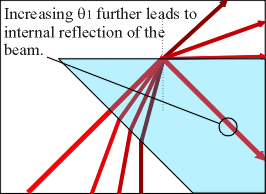
Rotate the source of laser light clockwise about the prism to increase the incident angle of the light hitting side C. Eventually the angle of refraction will be 90°, and the refracted beam will be transmitted along the interface of the plastic and the air. Further increasing the angle of incidence will turn the beam totally inside the prism - this is total internal reflection.
 |
 |
| Figure 3: Transmission through prism due to small incident angle |
Figure 4: Angles of incidence leading to total internal reflection |
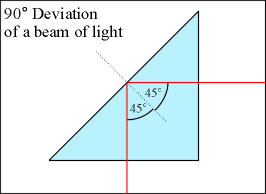
90° Deviation of a Beam of Light:
A right equilateral triangular prism whose critical angle, qc, is less than 45° can be used to deflect light at a right angle. Light shone normally on side A passes straight through, undeviated. Its angle of incidence on side C is 45°. This is greater than the critical angle, so the light is totally internally reflected. Since the angle of reflection is the same as the angle of incidence, the reflected ray moves off at 45° from side C's normal line. As you can see from the diagram to the right, the total deviation of the beam of light is 90°.
|
Figure 5: One case of Total Internal Reflection |
 Figure 6: Real life demonstration of figure 5.
|
180° Deviation of a Beam of Light:
Continuing its travel, the ray is incident on side A at 45°, so it reflects as it did when it hit side B. Now deviated a full 180° from its original angle, the light continues on to hit side C again. Because the direction of the beam has simply been reversed, the light hits C normally again, and so is not refracted as it passes back into the air again.
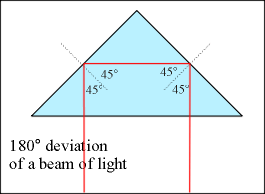 Figure 7: Two cases of Total Internal Reflection |
 Figure 8: Real life demonstration of figure 7
|
Apparatus:
- A right equilateral triangular prism
- A laser
- A small clear rod
Procedure:
Total Internal Reflection
- Place the right equilateral triangular prism on a flat surface.
- Shine the laser into side A of the prism such that the light is transmitted through side C.
- Rotate the source of laser light clockwise around the prism until no more light is transmitted through side C. All the light should be being reflected off side C and back into the prism. This is shown in the video below.
90° Deviation of a Beam of Light
- Point the laser normally on side A. The light should totally internally reflect off side C and back out side B. This deviates the light's path by 90°, as shown in the picture to the right.
180° Deviation of a Beam of Light:
- Shine the laser into side C so that it hits side A, reflects onto side B, then travels out side C again. The beam is thus deviated 180° from it's original path, as shown in the picture to the right.
SAFETY WARNINGS:
- Lasers can cause eye damage. Avoid exposure - never mount the laser at eye-level or point it toward reflective surfaces no matter how careful you are.