Wavelength & Frequency

The wave machine is used to show how the frequency and the wavelength of a wave depend on one another. 

WATCH THE VIDEO:

 Theory:

 

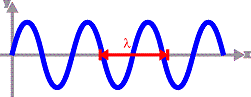
The wavelength of a wave is literally the length of one wave. It is the distance between one point on the wave and the nearest point where the wave repeats itself. The symbol for wavelength is λ.

The frequency of a wave is the number of complete waves that pass a point in a given time. It has the symbol f.

The frequency and wavelength are related to one another and to the speed of the wave by the following formula:

c = λf

If the speed of a wave is a constant (as it is in a single given medium), then waves with a larger frequency will have smaller wavelength, and waves with a smaller frequency will have a larger wavelength.

If a wave passes from one medium (where the wave speed is c1) into another medium which has a higher wave speed, c2, the frequency of the wave stays the same. Because the wave speed has increased, the wavelength must also increase to satisfy the above relationship.

 

Apparatus

• large and small wave motion machines
• damper
• small clamp

1. Set up the large wave machine on a flat surface.
2. Attach the damper to the last rod on the machine. This will decrease reflection and prevent interference from complicating the wave pattern.
3. Create low frequency waves.
4.  Then create higher frequency waves to show that the wavelength decreases. Try to use the same amplitude as when low-frequency waves were being created (to prevent students from thinking that the wavelength depends on the amplitude of the wave.
5. For the second part of this experiment, use the small metal clamp provided to join the large and small wave machines together at the ends.
6. Attach a damper to the last rod of the small wave machine.
7. Create waves on the large wave machine. The waves should increase in wavelength when they pass into the small wave machine.