Show conservation of angular momentum with student involvement.
Watch The Video:
Possible Incorporated Topics:
- Torque
- Vector addition
- Angular Momentum
Theory:
The basis of this demonstration is the conservation of angular momentum. As explained in, “Spinning on a stool” the initial angular momentum of a system must be conserved. The student starts off with no angular momentum sitting at rest on the stool. When handed the spinning bike wheel, angular momentum is introduced to the system but the total must still equal the initial value of zero. To do this, the stool spins in a direction as to create an opposing angular momentum to the wheel (see Figure 1)
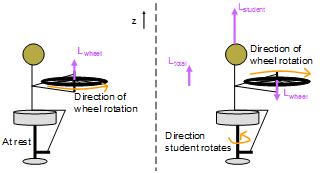
Fig. 1: Conservation of momentum of the student, stool and wheel system.
As shown in Fig. 1, the angular momentum in the z-direction is maintained. When the wheel is flipped so that it’s angular momentum is in the negative z-direction, the stool and the student spin counter-clockwise to create an upward angular momentum that cancels out a portion of the wheel’s downward momentum. As shown in the figure, the total angular momentum is equal to that which the wheel started with.
Apparatus:
- Bike wheel with extended central axle
- Rotating stool with foot rests
- Motor and grinder covered in rubber (option)
- Light student volunteer
Procedure:
- Pick a student volunteer with arms long enough to hold both ends of the wheel’s extended axle with the bike tire still being a safe distance from their body. Have the student sit on the stool and put their feet on the rests.
- Turn on the motor and grinder and holding the wheel by both ends of the extended axle, gently touch the wheel to the grinder to get it spinning. Once a sufficient speed is reached, remove the wheel from the grinder and turn off the motor.
- Hand the wheel to the student on the stool and also have them hold it by the central axle.
- Instruct the student to slowly rotate the wheel so that the extended axis is eventually vertical. The effects of the conservation of angular momentum should be very obvious by this point!
- Have the student turn the wheel back to the original position and then rotate it in the opposite direction as before. This can be repeated until the wheel slows to a stop.



