Spinning a Waiter's Tray (w/ bloopers)

How fast does a tray have to move so that a cup of water won't fall?

Watch The Video:

Bonus Blooper Reel!

Teachable Topics:

• Centripetal force
• Centripetal acceleration

Theory:

Newton's law says that a moving object will continue to move in a straight line at a constant velocity unless acted upon by an external force. An object moving in a circle would tend to fly off in a straight line, but is kept moving in a circle by a centripetal force. This is a force which is always directed in towards the centre of the object's circular path.

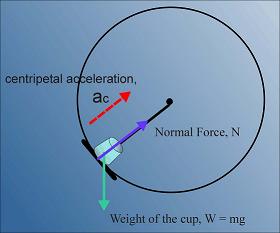
Figure 1: Centripetal acceleration

Although the moving object doesn't speed up, at each instant it is being accelerated towards the centre of its circular path. This acceleration is called a centripetal acceleration (a_c), and can be calculated from v (the magnitude of the object's velocity) and r (the radius of the circular path of the object) according to the following formula:

If a cup is placed on a tray that is being swung in a circular arc, how fast must the tray be swung so that the cup won't fall down when it's at the top of the loop? To answer this question, we need to examine the forces on the cup. These are the weight of the cup and the normal force of the tray table on the bottom of the cup.

At the top of the circular arc (where the cup is most likely to fall first), the forces on the cup look like this:

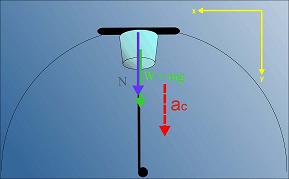
Figure 2: Forces acting on the cup

Using Newton's law to analyze the forces on the cup in the y-direction yields the following equation:

F_y = mg + N = ma_y

At this instant (when the cup reaches the top of its arc), the y-component of the accleration is the centripetal acceleration.

a_y = a_c = v²/r 

We now have that

mg + N = (mv²)/r 

Since the table is what pulls the cup in its arc, the normal force acts as the centripetal force. If the centripetal force (and thus the centripetal acceleration) is reduced until it is zero, the cup can no longer move in a circle... it will fall. Reducing the centripetal acceleration is accomplished by swinging the tray slower and slower (because ac is proportional to the magnitude of the velocity squared... less velocity, less centripetal accleration)

By reducing the centripetal force more and more, the normal force becomes closer and closer to zero. Then we have

mg = (mv²)/r

g = v²/r

The magnitude of the velocity must therefore be greater then this value for the cup to stay on the tray at the top of the arc.

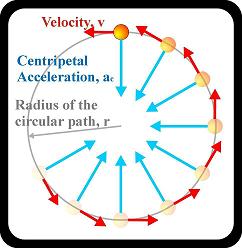Figure 3: Circular path of cup

Apparatus:

• Cup
• Tray with long handle
• Water

Procedure:

• Fill the cup with water and set it on the tray
• Swing the tray back and forth until you build up enough speed to swing the tray around and around in a complete circle
• After a couple of revolutions being to swing the tray more slowly until, eventually, the cup falls off the at the top of the arc

Tips: We recommend you practice this demo before you try to show it to anyone. It can take a few tries before you figure out the necessary speed required to spin the apparatus. It's also a good idea to use something other than a glass cup.