Bernoulli Floating Ball

A moving stream of air keeps a light ball suspended in mid-air, giving evidence for Bernoulli's equation.

WATCH THE VIDEOS

Other Demos of Interest:

Bernoulli Ping Pong Ball	Lifting Plates with Air Flow	How to Make a Vortex Cannon

Teachable Topics:

• Principles of flight
• Conservation of energy
• Air pressure

Theory

This follows this same principle as the Bernoulli's Ping-Pong Ball demo.

An ideal fluid is incompressible and flows steadily, irrotationally, and with no viscosity (or "fluid friction"). For our present purposes, it's important to note that "incompressible" means that the density of the ideal fluid is constant. Of course, real fluids like air and water are not so ideal, but in some situations the ideal fluid is a good enough model for these real fluids.

The equation that governs the flow of an ideal fluid is called Bernoulli's equation. This equation makes an interesting prediction about the relationship between the pressure and the speed of a moving ideal fluid. To discuss this prediction, we'll first need to understand the meaning of Bernoulli's equation, and we'll do this by looking at the following example.

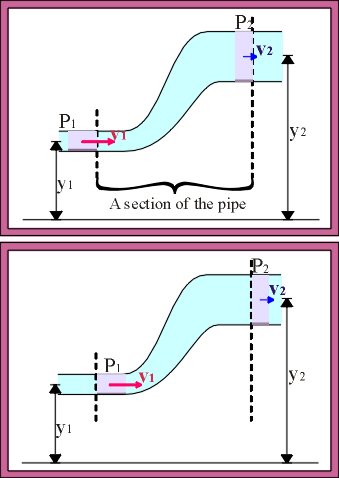
An ideal fluid with density ρ (Greek letter rho) flows steadily in a pipe. Over a time period Δt a certain volume of fluid (shown in pink) enters a section of the pipe. This volume of fluid flows in at height y₁, has pressure P₁, and moves at speed v₁.

In the same period, an equal volume of the same fluid flows out of the section of pipe. The volume of fluid leaving must be the same as the volume entering because the fluid is incompressible. The volume of fluid leaving leaves at height y₂ with pressure P₂ and speed v₂.

By applying the principle of conservation of energy, the following can be shown:

(Bernoulli's Equation)

Put another way,

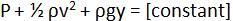
Here comes the interesting prediction. If air flows horizontally (y = constant), then we have 

Since our ideal fluid has constant density (ρ = constant), increasing the speed of the fluid must make the pressure decrease.

Even though we assumed that y = constant in making this prediction, this is not always a necessary condition - a fluid whose height changes often obeys the principle that a faster-moving fluid has a lower pressure.

To show the principle predicted by Bernoulli's equation in action, we'll create a steady, strong jet of air using a tube and a high-powered fan. If we place a ping pong ball in the stream of air, what happens? You might think the ball should topple off to the side, but it doesn't! The stream of air moves at high speed. As should be expected from Bernoulli's equation, this stream of air has a lower pressure than the stationary surrounding air. If the ball starts to move to one side of the stream, the high-pressure of the stationary air pushes it back into the stream.

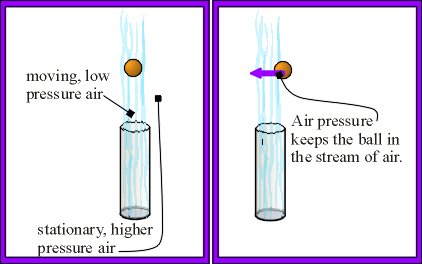
This effect is so strong that the tube can even be inclined without the ball falling. Gravity pulls the ball downward, but when the ball goes down far enough, the pressure difference between the top of the ball and the bottom is great enough to keep the ball aloft.

Apparatus:

• Air pump and hose
• Ping-pong ball

Procedure:

• Turn on the air pump and place the ball in the jet of air.
• Notice how the ball stays aloft.
• Try tipping the jet to show that keeping the ball aloft does not require that the stream of air hit the ball from directly below.