Description:
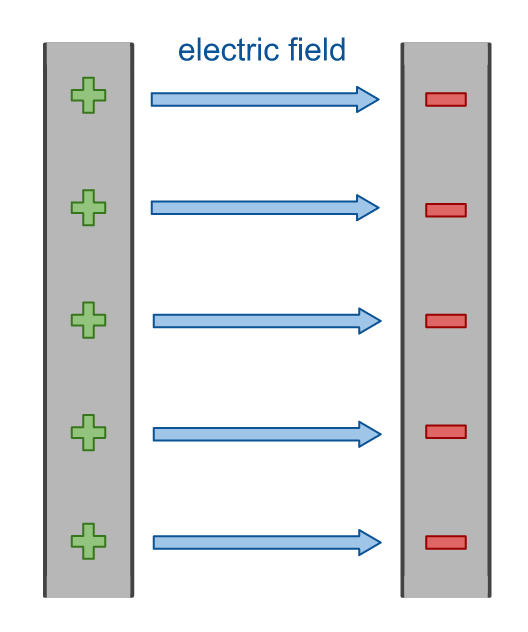
A capacitor is a basic circuit component that stores charge in its electric field.
Watch Video:
Other Demos of Interest:
Possible Incorporated Topics:
- capacitance
- RC circuit
- electric field
- electronics
Theory:
A capacitor is one of the basic components of a circuit (along with the resistor and inductor). A parallel-plate capacitor consists of two conducting plates of area A, separated by some distance (d) with an insulating or dielectric material between them. The dielectric increases the amount of charge that the capacitor can store. In this example, air is used as the insulator between the conducting plates.

Capacitors will charge and discharge when connected to a DC circuit. We can examine the behaviour of the capacitor by constructing the following RC circuit and measuring the voltage across the capacitor:
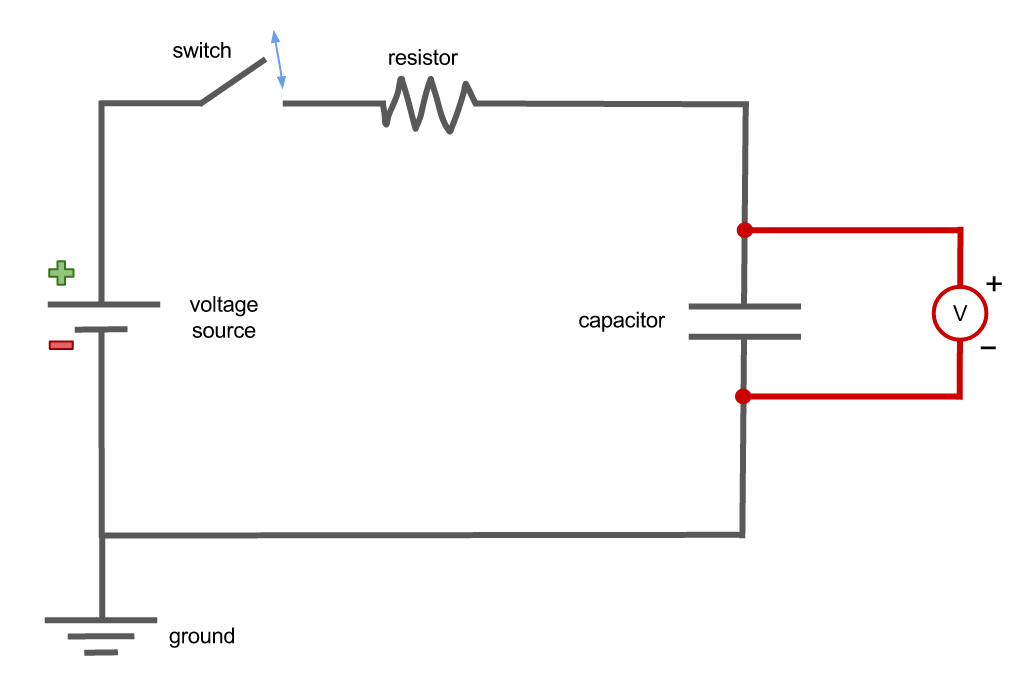
If the capacitor is initially uncharged, when the switch is closed and the circuit completed current will flow and the capacitor will begin to charge. Once the capacitor is fully charged, current will no longer flow. The capacitor will hold this charge, storing energy in its electric field to return to the circuit when required.
------------------------------
Capacitance is the ability of a body to store an electric charge. It is a measure of the the charge per voltage and is defined as:
![]()
where Q is the charge and VC the voltage of the capacitor.
Capacitance is measured in farads (F) which is Coulombs per Volt. 1 F is actually a lot of capacitance, so physical systems tend to deal in microfarads (1 μF = 10-6 F) or picofarads (1 pF = 10-12 F).
The capacitance of a parallel-plate capacitor is represented by:
![]()
where ε0 is the permittivity of free space constant, and k is the relative permittivity of the dielectric between the plates. This value is material-dependent, and is ~1 for air. The capacitance of a parallel-plate capacitor is thus purely geometric, depending only on the area of the conducting plates (A) and the distance between them (d). Plates that are larger and closer together thus have a higher capacitance.
------------------------------
The charging and discharging of the capacitor does not occur instantly; there is a time-dependence to the processes.
The charge of a charging capacitor obeys the following relationship:
![]()
While the charge of a discharging capacitor goes as:
![]()
The product RC is often called the time constant and written as:
![]()
The magnitude of the time constant dictates how fast the capacitor will charge and discharge. A circuit with a larger resistor and higher capacitance will take longer to charge and discharge. To charge and discharge the capacitor, the direction of the current must be reversed. Turning off the voltage supply will also cause the capacitor to discharge.
------------------------------

------------------------------
We can also examine the behaviour of the current (I) and the capacitor’s voltage (VC) as the capacitor charges and discharges.
In both cases, once the switch is closed current begins to flow at its maximum value. The amount of current exponentially decreases toward zero as the capacitor becomes charged/discharged and no longer requires any current to move the charge to/from the capacitor. The voltage follows the same curve as the charge when the capacitor charges and discharges.
The maximum values of charge, current, and voltage are defined as:
![]()
![]()
![]()
Apparatus:
- capacitor
- resistor
- voltage source
- oscilloscope
- connecting wires
Procedure:
- build an RC circuit and measure the voltage across the capacitor
- watch the capacitor charge exponentially when the voltage is turned on, and discharge exponentially when it is turned off






